Vivre et expérimenter les mathématiques à travers les arts et la culture (Atelier n°8)

Cet atelier s’adresse à toutes et tous, quelles que soient le degré de vos connaissances mathématiques, scientifiques et artistiques. Il s’agira avant tout de cultiver votre curiosité dans un esprit créatif et collaboratif.

Cet atelier vous incitera à porter un regard nouveau sur notre environnement, à y voir sur l’implication sous-jacente des mathématiques et des sciences, et à découvrir des domaines inattendus de la recherche.

L’atelier propose de vivre l’expérience des mathématiques a travers divers moments interactifs, de développer sa curiosité et sa culture mathématique et scientifique, d’inventer, concevoir, fabriquer, dans un cadre collectif et à travers les cultures et les arts, tout en développant des compétences informationnelles et médiatiques.

Une douzaine de rendez-vous nous permettront de mesurer l’influence des mathématiques sur notre société et dans notre quotidien au travers de sorties culturelles, de rencontres, d’ateliers, etc. Les futurs professeurs des écoles et les esprits plus scientifiques que littéraires y sont aussi les bienvenus.

Partenaire: Maison Poincaré – Institut Henri Poincaré

Restitution: Exposition et restitution en bibliothèque, événement ponctuel pendant la semaine des mathématiques

Groupe de travail sur la théorie des Nœuds

La théorie des nœuds est une branche des mathématiques appartenant à la topologie. Elle présente l'avantage de s'inspirer du monde réel. Elle consiste à étudier les nœuds tels qu'on les connaît dans la vie courante. Pour mieux définir ce concept et le rendre exploitable, on forme un nœud avec une corde, puis on relie ses deux extrémités afin qu'il ne puisse plus être défait de manière évidente. La théorie des noeuds trouve des applications dans de nombreux domaines (biologie et chimie, arts, informatique…)

Au cours de nos séances d’APAC, nous nous sommes penchés sur cette théorie, en nous demandant s’il était possible de rendre accessible ce domaine universitaire à des non connaisseurs. Nous interrogeant alors sur la vulgarisation des mathématiques, matière redoutée par beaucoup.

Groupe de travail sur le pavage des sphères

Nous avons choisi de travailler sur le pavage des sphères. Il s’agit de l’ensemble des portions de la surface d’une sphère dont l’union est la sphère entière, sans recouvrement. Ce sujet à fait émerger une problématique, nous nous sommes demandés quels polygones pouvaient paver une sphère ?

Nous avons donc commencé par tester tous les polygones qui permettent de paver une sphère. Nous tenons à souligner qu’il n’est pas possible de paver une sphère avec des formes planes. Nous faisons donc en sorte de nous approcher de pavages les plus réussis possibles avec le matériel que nous avons à notre disposition. L’objectif de notre travail est de trouver les différents polygones qui permettent de paver une sphère, leur trouver des points communs et, à terme, dégager une propriété.

Nous avons déjà testé plusieurs polygones qui fonctionnent (triangles (isocèles, équilatéraux), cerfs-volants, flèches, losanges) et qui ne fonctionnent pas (hexagone, pentagone, octogone).

Groupe de travail sur les flexaèdres à bases tétraédriques

Les flexaèdres sont des objets géométriques fascinants construits à partir de polyèdres qui défient nos intuitions en combinant rigidité et flexibilité. L’une des caractéristiques les plus étonnantes des flexaèdres est leur capacité à se retourner sur eux-mêmes permettant de transformer l'objet à travers une multitude de formes.

D'un point de vue mathématique, leur existence repose sur des principes mathématiques liés à la géométrie des polyèdres, aux transformations continues et à la cinématique des solides articulés. Les flexaèdres appartiennent à la catégorie des polyèdres flexibles, c'est-à-dire, des structures qui conservent leurs propriétés métriques et volumiques tout en étant capables de se déformer en maintenant les distances entre ses points fixes et ce de manière fluide sans jamais se briser ou se désassembler. Contrairement aux polyèdres rigides, qui ont des faces et des arêtes fixes dans l’espace, les flexaèdres présentent des charnières spécifiques qui permettent un mouvement continu. Particulièrement intéressants, les flexaèdres illustrent les principes des transformations continues et des mouvements dans l’espace. Ils sont également un exemple concret de la manière dont les propriétés géométriques peuvent être manipulées, tout en restant fidèles à la topologie de l’objet. Une transformation d’un flexaèdre ne modifie ni le nombre de faces ni leur configuration fondamentale ; ce qui change, c’est l’orientation et la position relative des faces les unes par rapport aux autres.

À travers cet atelier de pratique artistique et culturelle, nous nous efforçons d'explorer ensemble la construction de flexaèdres à partir de tétraèdres et de mettre en exergue les théories mathématiques qui en découlent.

Groupe de travail sur les MANDALA

Les mandalas sont des figures géométriques construites à partir d’une figure géométrique principale et de nombreuses autres formes pavant la forme principale.

L’intérêt de cet art mathématique est que toutes parts du diamètre se croisant au milieu forment un certain nombre d'angles identiques. Chaque part du cercle doit être identique à ce qu'on appelle “un motif”. Plus le mandala est complexe, plus les angles sont petits et plus le nombre d'axes de symétrie est grand. Il est même possible de faire des mandalas ayant plusieurs centres de symétrie axiale. Pour explorer le thème dans tous les domaines, il existe des mandalas faits à partir de pliages et des mandalas faits à partir d’un programme informatique. L'objectif est que tous les mandalas respectent les règles de base qui sont :

une symétrie centrale ;
un ensemble de forme géométriques ;
un motif répété dans chaque part de la forme principale ;
la forme principale doit être divisée par des droites passants au centre de cette forme et formant des parts identiques.

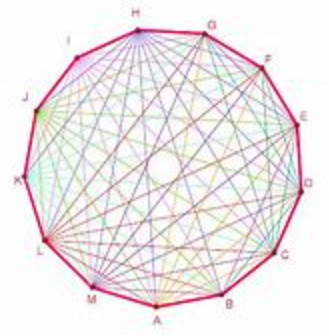
Groupe de travail sur les échecs

Le jeu d’échecs traditionnel est un jeu de société que l’on peut qualifier de jeu de guerre. Il oppose deux joueur.ses de part et d’autre d’un échiquier composé d’une grille carrée, dessinant 64 cases, alternant case claire et case sombre. Sur 32 cases sont disposées des pièces représentant les deux armées ennemies.

Le lien entre ce jeu et les mathématiques est encore plus étroit qu’il n’y paraît. En effet, on y retrouve des notions comme la loi binomiale, le nombre de Shannon, le théorème du cavalier… et l’échiquier lui-même représente une forme géométrique pensée. Sa dimension artistique est également indéniable tant son esthétique forte est connue de tous.tes.

Ainsi, nous nous sommes lancé.es le défi de modifier ce jeu pourtant si classique. Pour ce faire, nous en avons modifié l’échiquier en lui donnant une forme circulaire. Nous avons également retravaillé les pièces. Nous avons dû procéder à l’élimination du fou et du cavalier et nous avons modifié la disposition des pièces et leurs formes. Malgré les nombreuses modifications amenées, nous nous sommes essayé.es au jeu et la finalité reste similaire. Nous avions également pensé à la possibilité d’y ajouter un dé pour transformer ce jeu en jeu de hasard mais malheureusement, nous ne sommes pas allé.es au bout afin de ne pas modifier l’essence même de ce jeu.

Pour conclure, nous vous laissons avec deux problèmes en lien avec le jeu d’échecs, les mathématiques et tout ce qu’ils représentent…

Problème de Hamilton ou du cavalier : il est possible à l'aide d’une suite de déplacement de parcourir l’intégralité du plateau d'échecs avec un cavalier sans jamais repasser par la même case. Plusieurs solutions existent dont deux découvertes par Euler. Il semblerait aussi que certains mathématiciens arabes aient résolu le problème avant lui mais en Occident, son nom a été retenu.

Problème de l’échiquier de Sissa : un récit raconte l’histoire du prince indien Belkib capable d'exaucer un souhait à un.e de ses sujet.tes. Sissa demande alors au prince de déposer un grain de riz sur la première case, deux sur la deuxième, quatre sur la troisième et ainsi de suite pour remplir l’échiquier en doublant la quantité de grain à chaque case. A la fin, le prince Belkib se retrouve avec 2^64-1 grains de riz. Cette valeur est de l’ordre de 900 années de production mondiale de riz. Avec cette expérience, on se rend compte de l’importance des puissances en mathématiques.